 |
||
Каталог >> ИИ >> Новые свойства алгоритма исключения Гаусса и их применение для построения ньютоновских методов минимизации |
|
СВОЙСТВА АЛГОРИТМА ИСКЛЮЧЕНИЯ ГАУССА И ИХ ПРИМЕНЕНИЕ ДЛЯ ПОСТРОЕНИЯ НЬЮТОНОВСКИХ МЕТОДОВ МИНИМИЗАЦИИ А.Б. Хакимова, М.В. Свириденко Puma_home@mail.ru, MihaGod@mail.ru Содержание В статье излагаются: применение новых свойств алгоритма исключения Гаусса для построения направления спуска в ньютоновских методах минимизации; формирования подхода к минимизации псевдобулевых функций; формирование подхода для прогнозирования цен на товары, услуги и т.д. Приводится теоретическое и экспериментальное сравнение эффективности алгоритмов. Приведено обоснование, что построение направления спуска и псевдобулевое программирование, как и линейное, является частью линейной алгебры. В статье описываются новые свойства метода исключения Гаусса {Появление новых свойств метода исключения Гаусса отображаются как на развитии линейной алгебры, так и на построении новых алгоритмов математического программирования} и их применение для одновременного конструктивного построения {Описывает алгоритм построения по шагам}: · значения минимума квадратичной функции 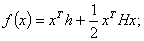 · координат 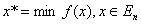 ; ; · аппроксимации 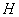 существенно положительно определённой матрицей
{То есть положительно определена и хорошо обусловлена. Последнее необходимо для численной устойчивости метода, поскольку
иначе округления при расчёте направления спуска на ЭВМ могут привести к тому, что мы получим направление, вдоль которого
минимизируемая функция не убывает}, если существенно положительно определённой матрицей
{То есть положительно определена и хорошо обусловлена. Последнее необходимо для численной устойчивости метода, поскольку
иначе округления при расчёте направления спуска на ЭВМ могут привести к тому, что мы получим направление, вдоль которого
минимизируемая функция не убывает}, если
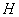 этим свойством не обладает; этим свойством не обладает; · преобразования координат для приведения 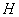 к диагональному виду; к диагональному виду; Настоящая работа содержит следующие основные результаты, как по теории линейной алгебры, так и по построению алгоритмов математического программирования: (i) Решение системы 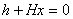 эквивалентно {Предполагается, что матрица эквивалентно {Предполагается, что матрица
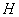 существенно положительно определена} решению задачи
{В курсе линейной алгебры в разделе «принцип Релея-Ритца и метод конечных элементов» приводится
основной результат, заключающееся в том, что решение системы существенно положительно определена} решению задачи
{В курсе линейной алгебры в разделе «принцип Релея-Ритца и метод конечных элементов» приводится
основной результат, заключающееся в том, что решение системы
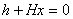 эквивалентно минимизации квадратичной формы эквивалентно минимизации квадратичной формы
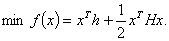 } } 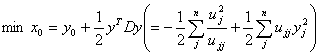 , , 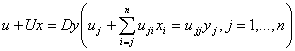 , , элементы 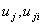 определяются пересчётом элементов определяются пересчётом элементов
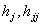 по рекуррентным соотношениям по рекуррентным соотношениям 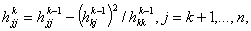 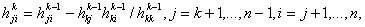 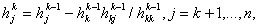 полагая 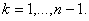 Здесь 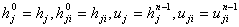 . . (ii) В процессе построения эквивалентной задачи методом исключения Гаусса в прямом порядке, перечисленные соотношения представляют всю необходимую информацию для аппроксимации матрицы 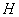 существенно положительно определённой матрицей, неявного масштабирования
шагов при спуске и для поиска направления отрицательной кривизны при появлении у минимизируемой функции седловой точки. существенно положительно определённой матрицей, неявного масштабирования
шагов при спуске и для поиска направления отрицательной кривизны при появлении у минимизируемой функции седловой точки.(iii) В процессе исключения Гаусса в обратном порядке приходим к построению новой эквивалентной задачи 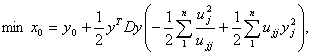 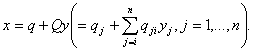 Здесь 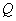 - верхняя треугольная матрица; матрицы - верхняя треугольная матрица; матрицы
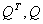 не ортогональные; не ортогональные;
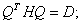
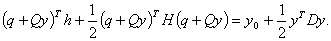 (iv) Эквивалентная задача достаточно проста и допускает усложнения для дальнейшего применения в линейной алгебре и математическом программировании. Рассмотрим, например, задачу, относящуюся к минимизации квадратичных функций на множестве булевых переменных. В этом случае эквивалентную задачу можно переписать в виде 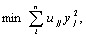 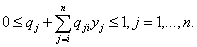 Очевидно, что только вершины многогранника, образованного ограничениями, формируют допустимое множество решений поставленной задачи. Отсюда следует, что оптимальное решение можно получить методом линейного программирования, а это означает, что псевдобулевое программирование (минимизация параболических функций {Псевдобулевую функцию можно определить как отображение 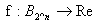 }
) является частью линейной алгебры. }
) является частью линейной алгебры.Можно выделить еще одну задачу, в которой используются ньютоновские методы минимизации, и, которая представляет практический интерес не только для предприятия, но и для нашего края. Это прогнозирование изменения цен на услуги, товары и так далее. Подход разработан в группе компаний «БЕРДЪ» г. Новороссийска и является естественным продолжением работы авторов [2]. Динамическая характеристика рынка недвижимости, включая задержку до начала реакции, имеет слишком большой разброс, чтобы моделировать поведение рынка с использованием обычной теории нелинейного регрессионного анализа. В данной работе рынок представлен физической динамической системой, которую можно считать неизвестным черным ящиком, имеющим один или более входов и выходов. На входы неизвестной системы и адаптивного фильтра подается один и тот же сигнал. Фильтр настраивается таким образом, чтобы его выходной сигнал соответствовал выходному сигналу неизвестной системы по критерию наилучшего среднеквадратического приближения. Близкое или вероятно полное приближение возможно тогда, когда адаптивная система имеет достаточное количество перестраиваемых весовых коэффициентов. Если входные сигналы изменяются в широком диапазоне и адаптивная система такова, что при подходящем выборе ее перестраиваемых параметров возможно такое моделирование, то процесс адаптации, минимизирующий среднеквадратическую ошибку, приводит к точному моделированию ее параметров. Изложение материала начнем с того, что в процессе исключения Гаусса в прямом порядке порождаются такие матрицы 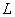 и и
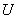 , что , что
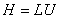 . Те же матрицы можно получить и, не пользуясь методом исключения Гаусса.
Равенства . Те же матрицы можно получить и, не пользуясь методом исключения Гаусса.
Равенства
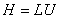 достаточно, чтобы определить их элементы. В скалярной форме это равенство
выглядит так; достаточно, чтобы определить их элементы. В скалярной форме это равенство
выглядит так; 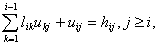 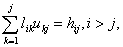 или, что то же самое, 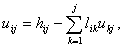 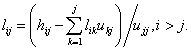 Легко видеть, что два последних соотношения позволяют с помощью элементарных арифметических операций поочерёдно вычислить строки матриц 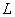 и и
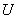 . Такой подход расчёта множителей . Такой подход расчёта множителей
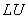 -разложения эффективен, когда -разложения эффективен, когда
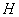 - симметричная положительно определённая матрица. В этом случае можно
обойтись без перестановок и сэкономить память, подбирая диагональные элементы матрицы - симметричная положительно определённая матрица. В этом случае можно
обойтись без перестановок и сэкономить память, подбирая диагональные элементы матрицы
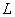
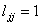 или так, чтобы было или так, чтобы было
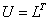 [2]. Данный подход положен в основу построения рекуррентных соотношений,
описанных выше. [2]. Данный подход положен в основу построения рекуррентных соотношений,
описанных выше. Напомним, что реализация одного шага ньютоновского метода условной или безусловной минимизации состоит из двух или трёх этапов {Представленная ниже схема описана Зойтендейком в 1970 году под названием метода «возможных направлений»}. На первом выбирается направление спуска. На втором определяется длина шага по выбранному направлению и новая точка. Третий этап, которого может не быть в конкретных алгоритмах, сводится к обработке информации, полученной в результате реализации первых двух этапов, для уточнения вспомогательных характеристик задачи, например оценок производных минимизируемой функции. Основной алгоритм численной линейной алгебры {Метод исключения Гаусса с частичным выбором ведущего элемента}, в дальнейшем метод исключения Гаусса (МИГ), представляет всю необходимую информацию для выбора направления спуска {См. работу авторов [3]} . От сюда следует, что для определения направления спуска средствами МИГ достаточно продолжить его построение, включая в его состав дополнительные блоки, например модели алгоритмов аппроксимации матрицы вторых производных {Матрица Гесса, в некоторых источниках Гессе} существенно положительно определённой матрицей, масштабирования при спуске, поиска направления отрицательной кривизны, учёта линейных ограничений, диагонализации матрицы вторых производных и т. д. Разработка дополнительных блоков связана с решением неравенств, поэтому продолжение построения МИГ переводит его на стык областей линейной алгебры (ЛА) и анализа. ЛА, в отличие от анализа, связана с решением уравнений и не имеет дела с неравенствами. Ньютоновские методы минимизации, как и линейное программирование, представляют собой контрпример: они связаны с неравенствами, но, безусловно, являются частью ЛА. Начнём с ньютоновских методов безусловной минимизации, в которых направление спуска 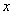 можно определить из условия минимума задачи квадратичного программирования
(КП) специального вида можно определить из условия минимума задачи квадратичного программирования
(КП) специального вида (1) 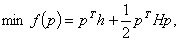
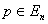 , , где 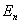 есть есть
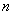 -мерное евклидово пространство. Градиент функции -мерное евклидово пространство. Градиент функции
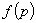 равен равен
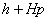 , и её минимум достигается при , и её минимум достигается при
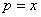 , где , где (2) 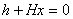 . . Перейдём в процессе исключения Гаусса в прямом порядке от (2) к эквивалентной системе (3) 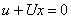 и, в процессе обратной подстановки, получим решение системы (1). Существенная положительная определённость матрицы 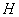 гарантирует разрешимость (2) относительно гарантирует разрешимость (2) относительно
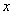 , а иначе вместо неё надо подставить матрицу, обладающую этим свойством. , а иначе вместо неё надо подставить матрицу, обладающую этим свойством.Авторами доказано следующее утверждение [3]. Пусть матрица 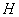 положительно определена, тогда существует конструктивное построение,
приводящее за n шагов задачу определения направления спуска к эквивалентной задаче в положительно определена, тогда существует конструктивное построение,
приводящее за n шагов задачу определения направления спуска к эквивалентной задаче в
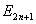 (4) 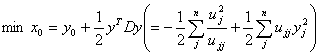 , , (5) 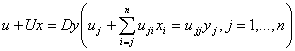 , , элементы 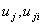 определяются пересчётом элементов определяются пересчётом элементов
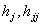 по рекуррентным соотношениям по рекуррентным соотношениям (6) 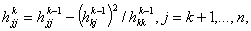 (7) 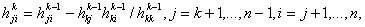 (8) 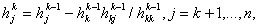 полагая 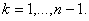 Соотношения (6)-(8) представляют всю необходимую информацию для аппроксимации матрицы 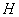 существенно положительно определённой, неявного масштабирования шагов при
спуске и для поиска направления отрицательной кривизны при появлении у минимизируемой функции Седловой точки. Для этого
требуется их слегка подправить по приведённым ниже правилам. Отсюда следует вывод, что конструктивное построение задачи
(4)-(5) является необходимым и достаточным условием для определения направления спуска. существенно положительно определённой, неявного масштабирования шагов при
спуске и для поиска направления отрицательной кривизны при появлении у минимизируемой функции Седловой точки. Для этого
требуется их слегка подправить по приведённым ниже правилам. Отсюда следует вывод, что конструктивное построение задачи
(4)-(5) является необходимым и достаточным условием для определения направления спуска. Следствие 1. Минимальное значение квадратичной функции 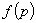 равно равно (9) 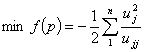 . . Следствие 2. Для определения направления спуска достаточно получить решение системы (5), полагая 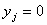 , например, в процессе обратной подстановки. , например, в процессе обратной подстановки. Следствие 3. для аппроксимации матрицы 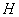 существенно положительно определённой матрицей существенно положительно определённой матрицей
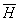 , достаточно в процессе исключения Гаусса в прямом порядке элемент , достаточно в процессе исключения Гаусса в прямом порядке элемент
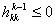 заменить элементом заменить элементом
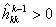 по правилу по правилу (10) 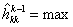
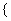
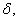
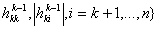 где параметр 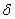 вводится для того, чтобы избежать численных трудностей поиска направления
спуска в случае плохой обусловленности матрицы вводится для того, чтобы избежать численных трудностей поиска направления
спуска в случае плохой обусловленности матрицы
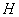 . При реализации алгоритма на конкретной ЭВМ, в которой под запись мантиссы
отводится . При реализации алгоритма на конкретной ЭВМ, в которой под запись мантиссы
отводится
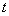 битов, величину битов, величину
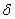 рекомендуется выбирать равной рекомендуется выбирать равной
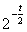 . . Для доказательства численной устойчивости необходимо и достаточно доказать, что правило (10) гарантирует, что величины элементов 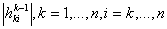 не могут быть произвольно большими. Авторами доказано следующее утверждение
[2]. Пусть не могут быть произвольно большими. Авторами доказано следующее утверждение
[2]. Пусть
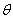
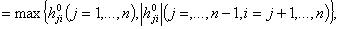 тогда правило (10) при пересчёте элементов тогда правило (10) при пересчёте элементов
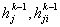 для для
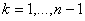 по рекуррентным соотношениям (6)-(8) гарантирует существование априорной
границы, такой, что по рекуррентным соотношениям (6)-(8) гарантирует существование априорной
границы, такой, что 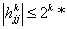
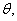
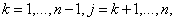 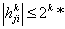
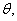
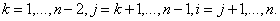 Предлагается следующий способ масштабирования шагов при спуске путём усложнения правила аппроксимации (10) 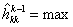
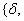
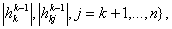 если 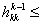
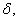 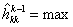
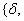
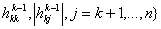 , , если 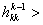
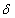 . . Экспериментальное сравнение эффективности правил аппроксимации показало, что учёт 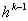 сокращает поиск оценки шага, удовлетворяющего условию существенного убывания
функции вдоль направления спуска. сокращает поиск оценки шага, удовлетворяющего условию существенного убывания
функции вдоль направления спуска. Предлагается следующий способ построения отрицательной кривизны. Пусть 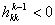 , тогда направление спуска можно найти, решая систему уравнений , тогда направление спуска можно найти, решая систему уравнений 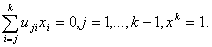 Теперь рассмотрим определение направления спуска на множестве линейных ограничений. Начнём с процесса исключения Гаусса в обратном порядке для перехода от задачи (4)-(5) к эквивалентной задаче в 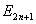 (11) 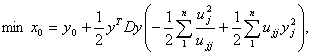 (12) 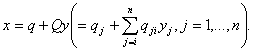 Отметим следующие свойства преобразования переменных (12): 1. 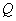 - верхняя треугольная матрица, - верхняя треугольная матрица, 2. Матрицы 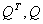 не ортогональные, не ортогональные, 3. 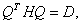 4. 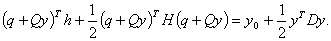 Подстановка (12) в ограничения приводит к задаче КП специального вида для поиска направления спуска. Из рекуррентных соотношений (3) - (5) и следствия 1 вытекает, что для расчёта спуска потребуется не более 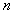 арифметических операций делений и арифметических операций делений и
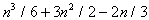 операций умножений и сложений. Описанная вычислительная схема расчёта
направления спуска является специализированным вариантом метода исключения Гауса для симметричных матриц. Она не требует
вычислений квадратных корней, дополнительной оперативной памяти и имеет более простую программную реализацию. операций умножений и сложений. Описанная вычислительная схема расчёта
направления спуска является специализированным вариантом метода исключения Гауса для симметричных матриц. Она не требует
вычислений квадратных корней, дополнительной оперативной памяти и имеет более простую программную реализацию.
Всюду и далее 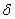
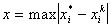 - точность решения по аргументам;
- точность решения по аргументам;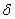
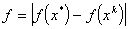 - точность решения по функции; - точность решения по функции;
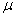 - число обусловленности - число обусловленности
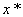 ; ;
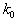 - число вычислений функции;
- число вычислений функции;
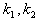 - соответственно число аппроксимаций матрицы вторых производных при наличии
отрицательных и нулевых собственных значений; - соответственно число аппроксимаций матрицы вторых производных при наличии
отрицательных и нулевых собственных значений;
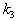 - число переходов к направлению отрицательной кривизны при появлении у
минимизируемой функции на очередной итерации седловой точки; - число переходов к направлению отрицательной кривизны при появлении у
минимизируемой функции на очередной итерации седловой точки;
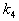 - число переходов к альтернативным направлениям спуска; - число переходов к альтернативным направлениям спуска;
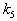 - число переходов к альтернативным направлениям спуска, приводящих к
уменьшению значений минимизируемой функции. - число переходов к альтернативным направлениям спуска, приводящих к
уменьшению значений минимизируемой функции. ЗАДАЧА 1. 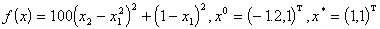 . Функция не выпуклая, имеет параболический овраг. . Функция не выпуклая, имеет параболический овраг. ЗАДАЧА 2. 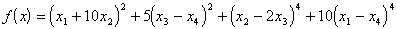 , ,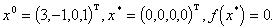 Функция не выпуклая, точка минимума - вырожденная ( Функция не выпуклая, точка минимума - вырожденная (
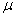 = =
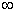 ). ).ЗАДАЧА 3. 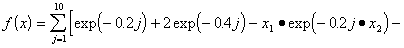 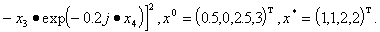 Функция не выпуклая, с искривлённым оврагом, обусловленность велика. Функция не выпуклая, с искривлённым оврагом, обусловленность велика. В таблице 1 приводятся результаты вычислений с помощью четырёх версий предлагаемого ньютоновского алгоритма безусловной минимизации - MNB01, MNB02, MNB03, MNB04. MNB01, MNB03 - соответственно алгоритмы без и с альтернативным поиском направления спуска без масштабирования по первой переменной. MNB02, MNB04 - соответственно алгоритмы без и с альтернативным поиском направления спуска с масштабированием по первой переменной. Все версии алгоритмов написаны на языке VISUAL BASIC 6.0, точность вычислений - одинарная. В таблице 2 приведены результаты вычислений с помощью общеизвестных методов, описанных в монографии Поляка Б.Т. Таблица 1 Сравнение предлагаемого алгоритма для задач 1-3
Таблица 2 Сравнение общеизвестных методов для задач 1-3
1. Стренг Г. Линейная алгебра и ее применения. Перевод с английского Ю. А. Кузнецова и Д. М. Фаге; Под редакцией Г. И. Марчука. Издательство «Мир», Москва, 1980. Тираж 14000 экз. 2. Хакимов Б. Б., Маилян А. А., Маилян А. А., Хакимова А.Б. Патент на полезную модель №51252. Система для обработки данных и управления рынка. Зарегистрировано 27 января 2006. Москва. 3. Хакимова А.Б., Хакимов Б.Б. Единый подход к решению задач математического программирования гуманитарной компьютерной клиники. Материалы I международной конференции «Системные, информационные и технические средства и технологии в профессиональной деятельности, образовании, оздоровлении и профилактике». Санкт-Питербург. Издательство СПбГПУ, 2003. 4. Уидроу Б., Стирнз С. Адаптивная обработка сигналов. Перевод с английского Ю. К. Сальникова; Под редакцией В. В. Шахгильдяна. Издательство "Радио и связь". Москва. 1989 год. Тираж 10000экз. 5. Numerical methods for constrained optimization. Edited by P. E. Gill and W. Murrey. National Physical Laboratory Teddington, Middlesex. Academic Press London , New York , San Francisco . 1974 .
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||