 |
||
БАЙЕСОВСКАЯ СТРАТЕГИЯ ПРОГНОЗИРОВАНИЯ РАЗНОТИПНОГО ВРЕМЕННОГО РЯДА НА ОСНОВЕ ВЫБОРКИ И ЭКСПЕРТНЫХ ВЫСКАЗЫВАНИЙ
В. М. Неделько
Институт математики СО РАН
Abstract. The task of prediction heterogeneous multidimensional time series is considered. The empirical information may be represented by both sample and statements of the experts. Using the statistical interpretation of the expert statements allowing to process unmatched or inconsistent statements, the method of constructing decision rules based on Byes approach is proposed. The case of structural variable space is also considered.
В работе рассматривается задача прогнозирования (продолжения) многомерного временного ряда (случайного процесса с дискретным временем) на основе информации о предыстории (выборки), а также экспертной информации, представленной набором несогласованных вероятностных высказываний нескольких экспертов.
При этом набор переменных, значения которых составляют временной ряд, предполагается разнотипным, то есть, переменные могут присутствовать одновременно непрерывные и дискретные, с упорядоченным и неупорядоченным множеством значений. Несогласованность экспертной информации предполагает, что высказывания могут быть в той или иной степени противоречивыми.
Для прогнозирования временного ряда строится решающая функция, отражающая вероятностные свойства изучаемого случайного процесса и представляющая собой оценку условного распределения в пространстве переменных прогнозируемого момента времени при заданной предыстории.
1. Постановка задачи.
Пусть
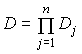 – пространство
значений, а
– пространство
значений, а Пусть зафиксировано
N+1 отсчетов времениИндексы, соответствующие отсчетам времени, будем размещать слева. Таким образом,
Для удобства записи предыстории введем также обозначения
Сформулируем задачу построения решающей функции.
Рассмотрим статистическую игру
Со стратегией природы
Будем предполагать, что вероятностные свойства процесса со временем не меняются, то есть
Задачу прогнозирования временного ряда можно решать через восстановление стратегии
c. При этом требуется указать алгоритмВ эмпирических данных могут одновременно присутствовать как реализация предыстории процесса, так и вероятностные высказывания экспертов, т. е. , где
Здесь
![]() , где
, где ![]() ,
, ![]() ,
,
![]() =
=![]() – оценка вероятности
попадания в
– оценка вероятности
попадания в ![]() при любом
при любом ![]() ;
; ![]() – оценка степени доверия высказыванию.
– оценка степени доверия высказыванию.
Для пояснения обозначений приведем пример экспертного высказывания:
“Если средний уровень оз. Байкал за прошлый год меньше 1700 (мм)
и суммарный годовой сток рек Баргузин и Селенга за прошлый год больше 800
или средний уровень оз. Байкал за прошлый год меньше 1650
и средний уровень оз. Байкал за позапрошлый год больше 1800,
то средний уровень оз. Байкал в текущем году прогнозируется
от 1500 до 1700 с вероятностью 0,4,
от 1700 до 2000 с вероятностью 0,3,
свыше 2000 с вероятностью 0,2,
менее 1500 с вероятностью 0,1;
уверенность 0,8”.
Обозначив ![]() = “средний уровень оз.
Байкал”,
= “средний уровень оз.
Байкал”, ![]() = “суммарный годовой сток рек
Баргузин и Селенга”, можем записать данное
высказывание в виде.
= “суммарный годовой сток рек
Баргузин и Селенга”, можем записать данное
высказывание в виде.
![]()
![]()
![]() .
.
Здесь
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]() , где
, где ![]() и
и ![]() – соответственно
минимальное и максимальное значения переменной Xj.
– соответственно
минимальное и максимальное значения переменной Xj.
При этом
2. Построение решающих функций.
Предлагаемый метод решения задачи состоит в получении апостериорной (при заданной эмпирической информации) вероятностной меры на стратегиях природы с использованием формулы Байеса:
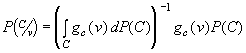 ,
,
где
Предположив, что эксперты делают высказывания независимо от имеющейся у нас выборки, имеем
Функция правдоподобия для выборочной реализации вычисляется как
Предполагая, это эксперты делают высказывания независимо, получаем
![]() .
.
Здесь
Для использования формулы Байеса осталось задать
Выберем подкласс
Меру
Представим
При этом
На множестве
После того, как апостериорное распределение на стратегиях природы получено, в качестве решения можно взять усредненную по данному распределению стратегию
3. Структурированное пространство.
Предложенный метод построения решающих функций может быть распространен для случая структурированного пространства переменных
[3], которое является обобщением разнотипного пространства, образованного декартовым произведением областей допустимых значений переменных на случай, когда объект исследования имеет сложную иерархическую структуру и когда диапазон значений некоторых переменных зависит от значений, принятых переменными верхнего уровня иерархии.Определение. Структурированное пространство переменных есть
либо интервал значений переменной с упорядоченным множеством значений,
либо подмножество значений дискретной переменной с неупорядоченным множеством значений,
либо декартово произведение структурированных пространств,
либо объединение непересекающихся структурированных пространств.
Данное определение подразумевает, что операции объединения и декартова произведения используются в конечном числе.
Пусть
Пусть
На
Класс измеримых подмножеств
Теперь изложенный метод построения решающей функции для прогнозирования временного ряда может быть перенесен на случай структурированного пространства переменных.
Действительно, для
Предложенный метод построения решающей функции прогнозирования временного ряда позволяет использовать разнородную эмпирическую информацию, представленную как обучающей реализацией временного ряда, так и высказываниями нескольких экспертов. При этом метод позволяет использовать в том числе противоречивую, информацию, автоматически согласовывая мнения различных экспертов.
Работа выполнена при поддержке РФФИ, проект № 980100673.
Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|