Будем рассматривать меру различия 2-х произвольных расстановок мест P_i и P_k для совокупности объектов A={a₁,...,a_N}.

1) поразрядную алгебраическую разность рангов r _ijI P_i, и r _kjI P_k (для j-го объекта, j=1,...,N):

d _i,k(j)=r _ij-r _kj;

2) число объектов n_D c различающимися рангами в расстановках P_i и P_k

3) номер объекта N_s с наивысшим изменяемым рангом в расстановке, принятой за базовую;

4) поразрядную сумму рангов:

S_i,k(j)=r _ij+r _kj;

D _i,k=D _i,k⁺+D _i,k^-;

6) число инверсий рангов (мест) I(P_i,P_k) в анализируемой расстановке P_k по отношению к расстановке P_i, принятой за базу сравнения;

7) удельное различие расстановок P_i и P_k: D_i,k= I(P_i,P_k)/ I(P_i,O P_i).

Под O P_i понимается инверсия расста-новки P_i, т.е. ранжирование её в обратном порядке.

Оценим с помощью приведённых показателей различие между произволь-ными расстановками мест P_i и P_k, выполненными в шкалах строгого и нестрогого порядка.

Сопоставление рейтингов в шкале строгого порядка характеризуется отношением r _max,i=r _max,k=N.

Рассмотрим 2 крайних случая соотношения рангов в расстановках P_i и P_k для 8-ми объектов через их разности d _i,k и суммы S_i,k:

1) P₀ =< 1, 2, 3, 4, 5, 6, 7, 8 >

P₀ =< 1, 2, 3, 4, 5, 6, 7, 8 >

d _0,0=< 0, 0, 0, 0, 0, 0, 0, 0 >

S_0,0=< 2, 4, 6, 8, 10, 12, 14, 16 >.

2) P₀ = < 1, 2, 3, 4, 5, 6, 7, 8 >

O P₀ =< 8, 7, 6, 5, 4, 3, 2, 1 >

d _0,0'=< -7, -5, -3, -1, 1, 3, 5, 7 >

S_0,0'=< 9, 9, 9, 9, 9, 9, 9, 9 >.

Отношение расстановки мест в лексико-графическом порядке P₀ самой к себе соответствует случаю полного совпадения расстановок (d _0,0=0 для всех объектов). Суммарные ранги сохраняют исходный порядок объектов: S_0,0(j)=2r _ij, j=1,...,N.

Соотношение лексикографического и антилексикографического порядков характеризует полное различие расстановок (P₀ и O P₀). В сумме они компенсируют друг друга, так как для всех объектов S_0,0=N+1.

Алгебраические суммы разностей рангов для пар расстановок (P₀,P₀) и (P₀,O P₀) равны 0: D _0,0 =D _0,0'=0. Это свойство распространяется и на пары произвольных расстановок.

Утверждение 1. Для любых 2-х расстановок P_i и P_k в шкале строгого порядка алгебраическая сумма разностей D _i,k равна 0: D _i,k=D _i,k⁺+D _i,k^-=0.

Это утверждение демонстрирует свойство сохранения сумм рассогласований рангов в 2-х расстановках. Суммарное приращение рангов для одних объектов компенсируется суммарным уменьшением рангов для других объектов совокупности.

Соотношению лексикографического P₀ и антилексикографического порядков O P₀ соответствует максимальное значение D_max =I(P₀, O P₀):

I(P_i,O P_i)= (1)

Величина I(P₀,O P₀) используется для нормализации различия порядков сопоставляемых рейтингов объектов. Для N=8, D_max=I(P₀,O P₀)=28.

Пример 1

P_i = < 2, 8, 3, 7, 6, 4, 5, 1 >

P_j = < 2, 7, 3, 4, 6, 5, 8, 1 >

d _i,j =< 0, 1, 0, 3, 0, -1, -3, 0 > Алгебраическая сумма разностей рангов равна: D _i,j =0, а n_D=4.

Определим I(P_i,P_j), упорядочив объекты по возрастанию мест:

P_i = < 1, 2, 3, 4, 5, 6, 7, 8 >

P_j = < 1, 2, 3, 5, 8, 6, 4, 7 >.

Здесь I(P_i,P_j)=5, N_s=4. Относительное различие расстановок P_i и P_j равно:

D_1,2=I(P_i,P_j)/D_max=5/28=0,18, а сходство: C_1,2=1-0,18=0,82

Шкала нестрогого порядка характе-ризуется отношением r _max<N. Причиной неравенства является наличие групп связанных рангов. Количество объектов, имеющих одинаковый ранг r , обозначим через nr (nr >1). Для двух сопоставляемых расстановок мест возможны следующие варианты соотношения шкал:

1. r _max,i=N, r _max,k<N;
2. r _max,i=r _max,k<N;

3) r _max,i<N, r _max,k<N, r _{max,i? r max,k}.

Первому варианту соответствует применение шкалы строгого порядка для одной расстановки и шкалы нестрогого порядка - для другой. В качестве предельного рассмотрим следующий случай:

P₀ = < 1, 2, 3, 4, 5, 6, 7, 8 >

P₁ = < 1, 1, 1, 1, 1, 1, 1, 1 >

d _0,1= < 0, 1, 2, 3, 4, 5, 6, 7 >

Расстановка P₁ имеет строгий лексико-графический порядок. Её максимальный ранг r _max,0=8 и все ранги не связаны: nr (P₀)=1, r =1,…,N. У расстановки P₁ r _max,1=1 и все ранги связаны: n₁(P₁)=8.

Алгебраическая сумма разностей рангов D _0,1=28>0. Её величина соответствует случаю полного различия порядков 2-х расстановок, т.е. D _0,0'=I(P₀,O P₀). Эту связь можно сформулировать следующим образом:

Утверждение 2. Максимальное рассогласование порядка в перестановке f(P₀,O P₀) равносильно отсутствию порядка в расстановке P₁:

I(P₀,O P₀)= D (P₀, P₁).

Очевидно, что в силу потери порядка мест в расстановке с нестрогим порядком P_i её нормирующий множитель D_max,н меньше нормирующего множителя D_max,с расстановки P_j со строгим порядком мест: D_max,н<D_max,с.

Величина I(P_i,O P_i) для произвольной расстановки P_i определяется по формуле:

I(P_i,O P_i)= 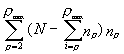(2)

Пример 2. Для упорядоченной в обратном порядке мест расстановки P_i:

P_i=< 5, 4, 3, 2, 2, 1, 1, 1 >

I(P_i,O P_i)=(8-5)2+(8-3)1+(8-2)1+(8-1)1=24.

Таким образом, при сопоставлении расстановок со строгим и нестрогим порядком мест в качестве нормирующего множителя принимается меньший: D_max,н<D_max,с.

Вариант соотношения шкал с r _max,i<N и r _max,i=r _max,k можно рассматривать как важный частный случай. Для него справед-ливо следующее утверждение.

Утверждение 3. Для 2-х расстановок P_i и P_k с r _max.i=r _max,k и n_j(P₁)=n_j(P₂), j=1,...,s, алгебраическая сумма разностей D _i,k равна 0: D _i,k=D _i,k⁺+D _i,k^-=0.

P_i = < 1, 1, 1 2, 2, 2, 2, 2 >

P_k= < 2, 2, 2, 2, 2, 1, 1, 1 >

d _i,k=<-1, -1, -1, 0, 0, 1, 1, 1 >

Расстановки P_i и P_k имеют одинаковые r _max=2 и числа элементов одного ранга в группах: n₁=3 и n₂=5. Суммы разностей рангов равны: D _i,k⁺=D _i,k^-=c 3c , а D _i,k⁺+D _i,k^-=0. Согласно формуле (2) D_max,н=15. Несмотря на противоположный порядок мест расстановки P_i и P_k имеют одинаковые ранги для 2-х объектов: N-n_D=8-6=2.

Степень различия рангов в нестрогой шкале по отношению к строгой можно оценить с помощью модуля различия рангов M. Для чётного числа объектов он вычисляется по формуле:

M = (3)

а для нечётного числа - по формуле:

M = (4)

Для расстановок с N=8 согласно формуле (3) M=16. В примере 3 степень различия рангов по отношению к строгой шкале равна: D _i,k⁺/M=3/16=0,19.

Выполним анализ 2-х расстановок, измеренных в разных шкалах нестрого порядка: r _max,i<N, r _max,k<N, r _{max,i? r max,k} на следующем примере.

P_i= < 5, 1, 7, 7, 6, 4, 2, 3 >

P_k=< 3, 1, 5, 6, 4, 3, 2, 2 >

d _i,k=<2, 0, 2, 1, 2, 1, 0, 1 >

Они имеют различие в рангах: n_D=6, D _i,k⁺=D _i,k=9, но не в порядках:

P_i= < 1, 2, 3, 4, 5, 6, 7, 7 >

P_k=< 1, 2, 2, 3, 3, 4, 5, 6 >.

Согласно формуле (2) D_max,k=23, но I(P_i, P_k)=0. Порядок мест в расстановке P_k более слабый за счёт r _max,i>r _max,k. Заметим, что различие рангов в расстановках P_i и P_k, начиная с места 3 (N_s=3), ещё не означает различия их порядков.

1. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. -М.: Высшая школа, 1989.
2. Липский В. Комбинаторика для программистов. -М.: Мир, 1988